DataBaseSQLD
데이터베이스설계 > ch7 (웹 보기)
📌 설계된 테이블 스키마를 Decomposition (분해)을 통해 Normal Form (정규형)으로 만드는 것, 테이블을 작은 단위로 분리하는 과정
↔ De-Normalization (반정규화)
- ❤️ 장점
- 데이터의 Consistency (일관성, 정합성), Integrity (무결성)
- 일반적으로 입력, 수정, 삭제 성능의 향상 (↔ 조회, 처리조건에 따라 다름)
- 💔 단점
- Entity 및 Relationship 개수 증가
- 과한 경우 조회 성능 저하 ⬅ 여러 번의 Join 필요
- 모든 정규화가 끝난 후, De-Normalization (반정규화)를 통해 개선 가능
Decomposition (분해)
📌 한 개의 테이블을 여러 개로 분리해는 것
- Redundancy (중복성) 제거를 위한 유일한 방법
- 분해된 테이블들의 경우, Join을 통해 원래의 값 찾을 수 있음
- 모든 분해가 좋은 것은 아님
- (Bad) Lossy Decomposition
- (Good) Lossless (무손실) Decomposition
Lossless (무손실)
📌 현실 세계에 없는 잉여 Tuple이 생기지 않는 것 (정확성이 손실되지 않는 것)
= 분해된 결과 테이블 간의 Natural Join의 Result Table이 분해 전 테이블과 동일한 특성 (Join을 통해 기존 테이블을 복구할 수 있는 경우)
= R = R1 ⋈ R2 (R = 스키마 = 컬럼의 집합)
= R1 ∪ R2 → R1 or R1 ∪ R2 → R2
- ⭐️ Decomposition (분해)의 필수 요건
Functional Dependencies (함수 종속)
📌 R = Schema의 모든 Columns 이고, α, β ⊆ R일 때, 시간의 흐름에 따라 Instance가 계속 바뀌더라도 α(결정자) 속성값이 같으면 항상 β(종속자) 속성값이 같은 특징 (α → β)
- 임의의 속성은 반드시 후보키, 슈퍼키에 함수 종속함 = Trivial (자명한 함수 종속)
- 특정 순간의 Instance Snapshot만으로 함수 종속 판단 불가, 항상 성립해야 함수 종속이라고 할 수 있음
Partial Functional Dependency (부분 함수 종속)
📌 후보키의 진부분집합 (= 후보키를 이루는 속성의 일부만으로 구성된 집합) → 키가 아닌 속성
= 일반 속성이 후보키의 일부에만 종속되는 경우
↔ Full Functional Dependency (완성 함수 종속)
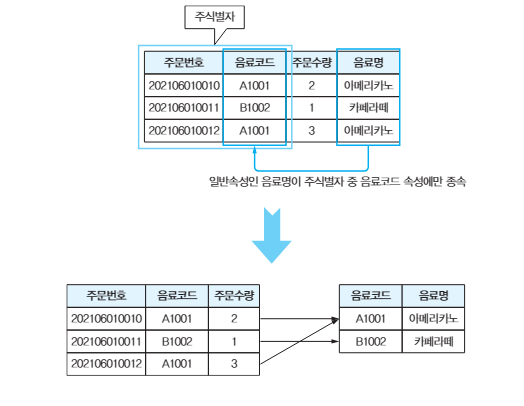
- 제 2정규형 (2NF) 대상
Transitive Functional Dependency (이행적 함수 종속)
📌 A → B이고 B → C인 경우 A → C
= B가 Identifier, Key가 아닌 경우 (즉, 키가 아닌 속성들 간 종속이 존재)
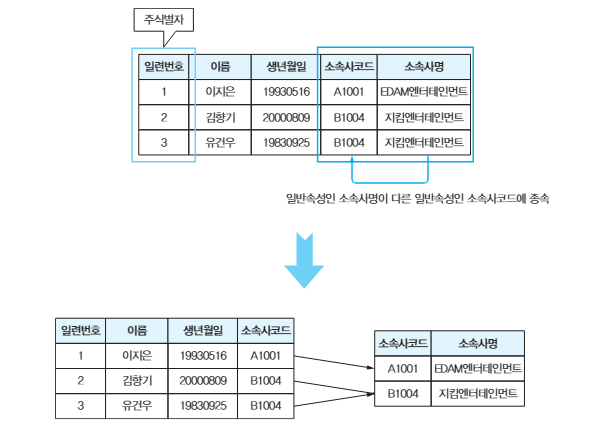
- 제 3정규형 (3NF) 대상
Closure (클로저)
📌 모든 함수 종속 F의 Transitive Functional Dependency (이행적 함수 종속)까지 망라한 집합 (F+)
Trivial Functional Dependency (자명한 함수 종속)
📌 β ⊆ α ⇒ α → β is Trivial
- 자기 자신은 항상 자기 자신의 결정자
↔ Nontrivial
Multivalued Dependencies (다치/다중값 종속)
Normal Form (정규형)
📌 정해진 특정 제약 조건을 만족하는 형태의 Relation
- 제 3정규형 (3NF) 또는 BCNF 형이 되도록 정규화 필요

제 1정규형 (1NF)
📌 모든 테이블 속성값이 Atomicity (원자성)을 가지는 형태
= 모든 속성이 하나의 값만 가지는 형태
- 상황
- 다중값 속성, 속성에 여러 속성값이 들어가는 경우 (🔎 직업 - 배우, 가수, 작곡가)
💔 Split 등의 파싱 과정을 거쳐야 함, 특정 속성값을 갖는 인스턴스 추출 어려움 - 유사한 속성이 여러 개인 경우 (🔎 사이트 1, 사이트 2, …)
💔 속성이 계속 추가되어야 할 수 있음, 속성값 개수 적은 인스턴스의 경우 공간 낭비
- 다중값 속성, 속성에 여러 속성값이 들어가는 경우 (🔎 직업 - 배우, 가수, 작곡가)
제 2정규형 (2NF)
📌 1NF에서 Partial Functional Dependency (부분 함수 종속)을 제거한 형태
= 모든 속성이 일부 후보키에만 종속되지 않는 형태
Lossless (무손실) 분해
📌 하나의 Relation을 분해하여 두 Relation을 만들었을 때, 이 둘을 다시 Join하여 원래의 Relation의 정보를 완전하게 얻을 수 있는 분해
- 특정 조건을 만족하지 않는 모든 함수 종속 α → β에 대해,
- R ➡
α ∪ β,R - (β - α)로 분해 - 새 테이블
R - (β - α)에 대해, 다시 조건을 검사해본 후 계속 분해
(= 부분 함수 종속에 대해, 결정자와 종속자만을 Column으로 갖는 테이블과 원본 테이블에서 종속자만 뺀 테이블 두 개로 분리)
- R ➡
제 3정규형 (3NF)
📌 2NF에서 Transitive Functional Dependency (이행적 함수 종속)을 제거한 형태
= 키가 아닌 속성들 간의 종속이 없는 형태
β - α안의 각각의 속성이 후보키
BCNF
📌 최대한으로 함수 종속성을 배제한 상태, 모든 F+의 함수 종속이 두 가지 조건 중 하나를 만족하는 형태
- Trivial (
β ⊆ α) - Nontrivial && 결정자가 후보키 (Unique)