정렬

AlgorithmSort

1. 선택 정렬: i ~ n까지의 값 중 가장 작은 것을 선택하여, i와 swap (n^2)
   • 정렬된 게 앞쪽에 모임
2. 삽입 정렬: 2번째 값부터, i번째 값을 0 ~ i-1 사이에 끼워넣고, shift (n^2)
   • 정렬된 게 앞쪽에 모임
3. 버블 정렬: 0번째 값부터 바로 뒤의 값을 0 ~ (n - i)번째까지 확인하며, 바로 뒤의 값과 swap해가며 정렬 (n^2)
   • 정렬된 게 뒤쪽에 모임, 구현 가장 쉬움
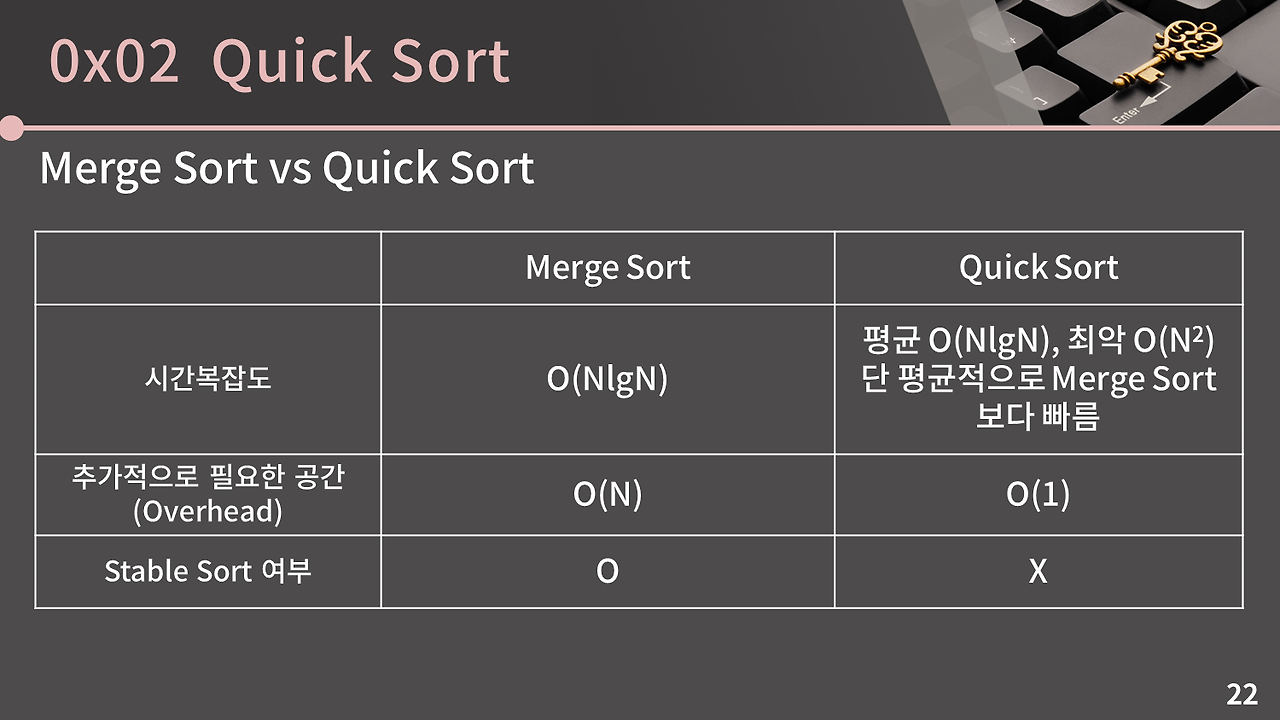
4. 병합 정렬 Merge Sort: 배열을 1/2로 나눠 정렬한 뒤 (재귀, D&C), merge (맨 앞쪽 포인터를 살펴가며 1 scan) (항상 nlogn)
   • ⭐ 정렬을 직접 구현해야 할 경우, 퀵 정렬이 아닌 병합 정렬을 구현해야 함
     
5. 힙 정렬: 정렬 순서와 반대되는 Heap을 만든 뒤, n ~ 0까지 swap 후 힙 정렬 (nlogn)
   • 힙의 root를 맨 마지막 node와 swap해서, 배열의 맨 뒤부터 정렬
6. 퀵 정렬 Quick Sort: 나눌 배열의 맨 앞을 Pivot으로 설정하고, Pivot보다 작은/큰 배열로 절반을 나눈 뒤 각 절반에 대해 또 반복 (nlogn, 이미 오름/내림차순 졍럴되어 있는 최악의 경우 n^2)
   1. 포인터 초기화 (= Pivot 제외 배열의 양 끝)
      • left = Pivot + 1 = 1
      • right = n - 1
   2. left가 가리키는 값이 Pivot보다 클 때까지 이동
   3. right가 가키리는 값이 Pivot보다 작을 때까지 이동
   4. left ⇐ right (교차하기 전): swap(s[left], s[right]) 후 left, right 이동 🔃
   5. left > right (교차한 이후)
      • right가 가리키는 값 = left 배열의 바지막 원소
      • swap(s[0], s[right]) 후 Pivot = right 리턴
   • ⏰ n
7. 트리 정렬: 이진 탐색 트리를 만든 뒤, 중위 순회하여 정렬 (nlogn)
8. Counting Sort: 수가 등장할 때마다 각 수를 인덱스로 하는 배열 원소의 값을 1씩 더하면서 각 수의 개수를 세고, 이 정보를 토대로 정렬 (⏰ n, 🏚 n)
   • ⭐ 등장할 수 있는 모든 수의 개수를 셀 수 있을 크기의 배열을 선언해야 함
     1. 정수만 가능, 음의 정수를 포함할 경우 별도 처리 필요
     2. 수의 범위가 한정적일 때 (1000만 이하)
     3. 숫자의 중복이 많을 때
9. Radix Sort (기수 정렬): 원소를 k진수로 취급하며, 1의 자릿수부터 d번째 자릿수까지 각 자릿수에 대해 0~k을 범위로 Counting Sort 수행 (⏰ dn, 🏚 nk)