Index (인덱스)

📌 특정 값을 가리키고 있는 포인터를 통해, 각 아이템에 대한 빠른 참조를 제공하는 방법

Multiple Key Access의 경우, Query 조건에 따라 성능 개선에 인덱스가 도움되지 않는 경우 존재
- 성능에 도움이 되더라도, Query 빈도와 Update 빈도를 살펴보고 선택 필요 (인덱스 관리 및 공간 Overhead와의 Trade-Off)
Unique한 속성의 경우, 고유 식별성 판단을 위해 자동으로 생성되기도 함 ➡ Integrity Constraint (무결성 제약), 검색 효율

구현

	B+ Tree	B Tree	Hash
특징	Leaf에만 Search Key 존재	NonLeaf 또한 Search Key
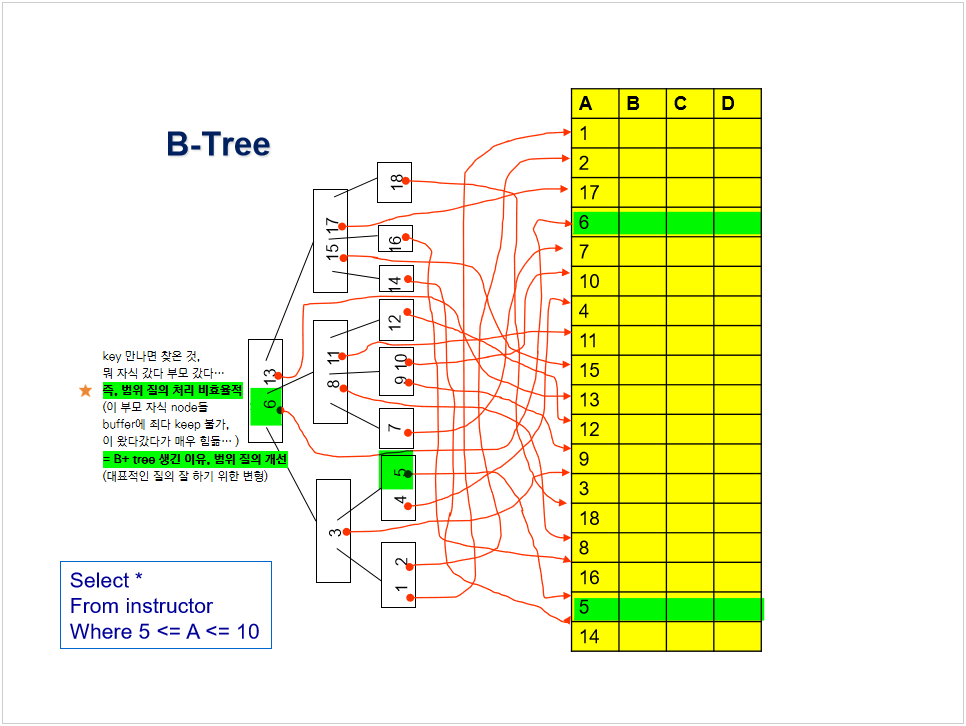
장점	⭐ 목적 = Range Query의 개선	Exact Match Query의 경우, NonLeaf에서 발견 즉시 탐색이 종료됨	Exact Match Query의 경우, B+ Tree보다 더 효율적
단점	무조건 Root Tree에서부터 탐색해야 함	1. 비효율적인 Range Query 2. NonLeaf에도 Pointer가 있어야 하므로 Fanout이 작아짐 ➡ Tree 높이가 높아짐 3. 복잡한 구현	1. Range Query 어려움

Clustered/Primary Index
1. Leaf가 Pointer로 Record의 Slot 가리킴
2. Covering Index: Leaf에 일부 데이터 저장 + Pointer
3. (B+ Tree File Organization) 전체 Record 내장
Non-Clustered/Secondary Index
1. Leaf가 Pointer로 Record의 Slot 가리킴
2. (Primary가 B+ Tree File Organization일 경우) Leaf에 Pointer 대신 Primary의 Search Key를 줌
  - 이 경우 Node가 계속 분할 및 병합되므로, Slot을 가리키게 되면 위치가 계속 바뀌어 댕글링 포인터가 될 것
  - Tree 탐색을 2번 해야 함 ➡ Primary보다 성능 별로

↔ Ordered Index, B+ Tree의 Leaf Node처럼 Search Key가 순서대로 정렬되어 있지 않음

Static Hash: 저장할 공간의 크기 미리 설정
- Bucket Overflow: 해시 Collision이 발생했고, 해시값에 해당하는 버킷 용량이 다 차서 더는 저장할 수 없는 경우
  1. Open/Closed Addressing/Hashing: 남아 있는 버킷을 순서대로 따라가며, 빈 공간 있을 경우 이를 활용 = Linear Probing
    - Main Memory 기반 Hash
  2. ⭐ Chaining: Overflow 버킷이 있을 경우, 새 버킷을 생성한 뒤 Chaining (Linked List)를 통해 원본 버킷과 연결
    - Secondary Memory 기반 Hash
- 문제: 지나친 Grow/Shrink ➡ 과도한 Chaining, O(1)에 Record 탐색 불가
  - 해결: Hash Func 재설정 + 버킷 재배치 (Expensive, 서비스 잠시 중단)
⭐ Dynamic Hash
- 목적: Overflow Bucket Chaining이 너무 길어지지 않도록 DB의 Grow/Shrink에 대응하기 위해
1. Linear Hashing: Hash Func가 동적으로 변화 + 버킷 한 개 추가
  - k mod n ➡ k mod 2n
2. Extendable Hashing: Hash Func가 주는 Bit Pattern의 뒤쪽 길이를 2배로 증가 + 해시값에 매핑되는 각 버킷 2배로 증가

📌 각 Discrete Value에 대해 Bitmap을 생성하여, 해당 Value를 갖는 Record가 있을 경우 Record 번호에 해당하는 Bit를 1로 설정

전제
1. Record 번호를 통해, 바로 Record를 탐색할 수 있는 파일 구조 필요
2. 삽입/삭제가 덜 빈번한 경우
  - 삭제의 경우, 삭제 Bitmap에 표시해둔 뒤 AND 연산으로 해결 가능
조건
1. Domain에 Discrete Value가 적은 종류만 존재할 때 ➡ Bitmap 개수가 줄어듦, 공간 효율
2. Where절에 AND로 여러 조건을 중첩해야 할 때 ➡ 각각에 해당하는 Block을 다 Buffer로 불러오지 않고, Bit 연산으로 Block 개수를 추릴 수 있음
3. Select절에 집계함수가 활용될 때 ➡ Record를 뽑아오지 않고 Bit 개수를 통해서만 계산 가능
❤️ 공간 효율